La produzione
Si definisce produzione l'attività volta a trasformare gli input (fattori di produzione) in output (prodotto).
La funzione di produzione è un'espressione matematica che descrive la relazione tra il prodotto (output) e i fattori di produzione (input) necessari a produrlo. Per semplificare, i fattori di produzione sono ridotti a due: il capitale e il lavoro. Un'espressione generica di funzione di produzione potrebbe essere, per esempio,
.
•Saggio marginale di sostituzione tecnico (SMST)
Il saggio marginale di sostituzione tecnico è la trasposizione nell'ambito della teoria della produzione del concetto di saggio marginale di sostituzione presentata in riferimento alle scelte di consumo. Si consideri una funzione di produzione, che utilizza due input, x e z, per produrre l'output y. Il SMST tra il fattore produttivo x e il fattore produttivo z rappresenta l'ammontare del fattore z che si può sottrarre dal processo produttivo, a patto di impiegare un'unità in più del fattore x e permanere con un livello di produzione invariato. In altre parole il SMST rappresenta la possibilità di sostituire un fattore con un altro, a parità di produzione ottenuta. Analiticamente il SMST è dato dal rapporto tra le produttività marginali dei due fattori.
Se ogni fattore ha produttività marginale decrescente, allora il SMST è decrescente; questo intuitivamente significa che - a parità di produzione ottenuta - un'unità di un input è tanto più “preziosa” in termini di sostituibilità con l'altro input, quanto meno se ne sta utilizzando. A ciò corrisponde un isoquanto convesso (ossia ben conformato). Nel caso di funzione di produzione lineare in tutti i fattori, invece, il SMST è costante, ossia il rapporto di sostituibilità tra i fattori non dipende dalla quantità di fattori che è già impiegati nel processo produttivo.
•Rappresentazione grafica di una funzione di produzione
Graficamente l'insieme delle combinazioni di due input necessarie a produrre un certo quantitativo di output, nell'ipotesi che gli input siano buoni sostituti l'uno dell'altro, è rappresentabile mediante un isoquanto simile a quello presentato nella fig. 9.1. Ogni punto sulla curva rappresenta una determinata combinazione di x
Se gli input fossero sostituti perfetti l'isoquanto sarebbe lineare (vedi figura 9.2), se invece ci fosse complementarietà tra gli input l'isoquanto risulterebbe ad angolo retto come nella figura 9.3.
Ognuno dei due fattori (x
Media correlati
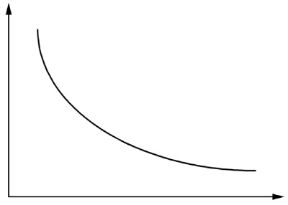
Figura 9.1 Un tipico isoquanto convesso. In queso caso il saggio marginale di sostituzione tecnico è decrescente.
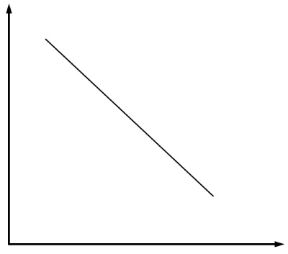
Figura 9.2 Isoquanto lineare.
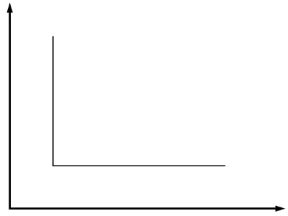
Figura 9.3 Isoquanto ad angolo retto.
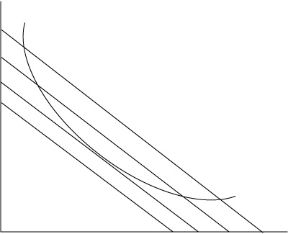
Figura 9.4 La combinazione dei fattori x


