La difficile ricerca di un equilibrio in un mercato oligopolistico
Tra le più note teorie dell'oligopolio vi sono quelle di P. Sylos-Labini e F. Modigliani, che fanno riferimento al prezzo di eliminazione (costo variabile medio di produzione maggiorato di un saggio normale di profitto) e al prezzo di esclusione (costo totale medio di produzione maggiorato di un saggio normale di profitto) valutato dalle imprese già presenti sul mercato oligopolistico al fine di difendersi dalla concorrenza potenziale. Con tali prezzi, esse abbandonano almeno temporaneamente il principio di massimizzazione del profitto, accontentandosi di un basso saggio di profitto, per praticare un prezzo più basso tale però da disincentivare le concorrenti potenziali dall'entrare sul mercato (prezzo di esclusione), o tale da indurre quelle già presenti all'uscita (prezzo di eliminazione).
•Modelli matematici dell'oligopolio
Due sono i modelli maggiormente applicati all'oligopolio: quello di A. Cournot e quello di J. Bertrand. Il modello di Cournot si caratterizza per la presenza di poche imprese, due nel caso più semplice (duopolio), che massimizzano il proprio profitto scegliendo in via strategica la quantità da produrre, supponendo che le rivali non varino la propria quantità in reazione alla propria scelta.
I beni prodotti sono perfettamente omogenei, per cui non è possibile osservare scostamenti tra i prezzi praticati dalle imprese. I consumatori sono numerosi e non hanno alcun potere di mercato; il loro comportamento aggregato determina il prezzo a cui si venderà la merce.
•Il modello di Cournot
Il modello di Cournot, elaborato dall'economista francese Augustin Cournot nel 1838, costituisce il primo esempio di modello matematico di duopolio. In un mercato con un prodotto omogeneo si ipotizza che due imprese competano con l'obiettivo di massimizzare il proprio profitto, e nel decidere la quantità da produrre ogni impresa prenda come un dato la quantità offerta dal rivale. Sulla base di questa ipotesi di comportamento – la cosiddetta congettura cournotiana – si dimostra che l'equilibrio di mercato si ottiene quando le quantità offerte dalle due imprese e assorbite dal mercato, data la curva di domanda, sono tali che nessuna delle due imprese possa aumentare il proprio profitto variando la propria offerta, essendo data la quantità del rivale. Per risolvere il problema di Cournot possono essere utilizzate le curve di reazione, cioè i grafici delle funzioni di reazione, che esprimono per ogni impresa le quantità ottimali in funzione della quantità offerta dal rivale (vedi figura 12.1). Gli equilibri di Cournot possono essere individuati geometricamente dalle intersezioni delle curve di reazione dei duopolisti, e, supponendo che in un certo istante le imprese producano quantità che non siano di equilibrio, si può descrivere il processo di aggiustamento verso l'equilibrio e valutarne l'eventuale stabilità. Il modello è stato esteso anche al caso di un mercato con numerose imprese e si è dimostrato che al limite, se il numero di imprese tendesse all'infinito, l'equilibrio di Cournot tenderebbe all'equilibrio che caratterizza un mercato perfettamente concorrenziale.
Il duopolio è un mercato oligopolistico in cui competono tra loro solo due imprese.
La congettura cournotiana, secondo la quale ciascuna impresa assume che la quantità prodotta dai rivali sia un parametro, è stata criticata per il suo scarso realismo e perché, quando estesa alla versione dinamica del modello di Cournot, implica che gli agenti non imparino nulla dall'esperienza. Dalle critiche al modello di Cournot sono scaturiti altri modelli di duopolio, come quelli di Bertrand e di von Stackelberg nonché elaborazioni più complesse nell'ambito della teoria dei giochi.
•Il modello di Bertrand
Quello di Bertrand, è un modello di duopolio presentato dal matematico francese Joseph Bertrand in un saggio sull'opera di Cournot nel 1883.
Nel modello di Bertrand si ipotizza che la variabile strategica ai fini dello studio del comportamento delle imprese e degli equilibri di mercato sia il prezzo e non la quantità, come invece assunto nel modello di Cournot. Più in generale, si parla di concorrenza alla Bertrand con riferimento ai modelli di duopolio o di oligopolio in cui le imprese competono per stabilire i prezzi e il mercato determina poi la quantità venduta.
Quando un'impresa determina il prezzo, con l'obiettivo di massimizzare il proprio profitto, deve prevedere anche il prezzo scelto dai concorrenti. Nel caso di due imprese che abbiano costi marginali costanti e uguali e che vendano un identico prodotto, come è quello descritto nel modello originario di Bertrand, l'equilibrio di mercato coincide con quello di concorrenza perfetta, ovvero le imprese fissano il prezzo a un livello pari al costo marginale. Infatti, supponendo che l'impresa 1 possa diminuire il proprio prezzo di una piccola quantità rispetto al prezzo stabilito dall'impresa 2, tutti i consumatori preferirebbero acquistare dall'impresa 1, ovvero, diminuendo il prezzo anche di una quantità arbitrariamente piccola l'impresa 1 potrebbe sottrarre tutto il mercato all'impresa 2. Poiché questo ragionamento vale anche per l'impresa 2, ne consegue che l'unico equilibrio possibile in questo caso è quello concorrenziale, dato che a nessuna delle due imprese conviene scendere al di sotto del costo marginale. Questo risultato costituisce il cosiddetto paradosso di Bertrand: come può il prezzo essere concorrenziale se sul mercato sono presenti solo due imprese? La soluzione di questo paradosso può essere ottenuta rimuovendo le tre assunzioni cruciali del modello, e cioè: introducendo l'ipotesi di due prodotti differenziati, anziché di un solo bene omogeneo; modificando l'ipotesi sulla funzione di costo (per esempio, introducendo vincoli di capacità); supponendo che le imprese possano colludere anziché agire in modo indipendente e non-cooperativo.
•Il modello di Stackelberg
È un modello di duopolio che esamina le interazioni fra un'impresa leader e un'impresa follower, formulato dall'economista H. von Stackelberg (1934). È detta leader l'impresa che fissa il proprio prezzo (leader di prezzo) o la quantità da produrre (leader di quantità) prima della concorrente; quest'ultima è detta follower di prezzo o di quantità. L'interazione strategica fra le due imprese avviene in modo sequenziale, in quanto il follower determina il proprio prezzo o il livello di output, data la scelta del leader: questa situazione nella teoria dei giochi, è un esempio di gioco sequenziale.
Spesso il modello di Stackelberg è utilizzato per descrivere i mercati in cui esiste un'impresa dominante, che rappresenta il leader, e altre imprese satelliti, di piccole dimensioni, che si comportano come follower. Supponiamo che il leader e il follower producano un identico bene. Consideriamo dapprima il caso in cui le decisioni delle imprese riguardino la quantità da produrre. Il profitto del follower dipende dal livello di output già determinato dal leader e dunque percepito come una costante da parte del follower. Pertanto, il follower determina il livello di output in modo da massimizzare il proprio profitto, data la scelta del leader. Quest'ultimo, d'altra parte, sapendo che le proprie azioni influenzeranno la scelta del follower, determina il proprio livello di output, incorporando la funzione di reazione del follower nella propria funzione di profitto. Rispetto alla soluzione che si otterrebbe se le imprese si comportassero come nel modello di determinazione simultanea delle quantità prodotte di Cournot, qui il livello di output e i profitti sono maggiori per il leader, che gode di un “vantaggio della prima mossa” e minori per il follower. Se, invece di stabilire la quantità, il leader fissa il prezzo, quest'ultimo verrà considerato come un dato dal follower: esso, in questo caso, si comporta come se fosse un'impresa concorrenziale, in quanto sceglie il livello di output che corrisponde al profitto massimo, dato il prezzo. D'altra parte, il leader determina il prezzo e il livello di output che gli consentono di massimizzare il profitto, incorporando l'informazione relativa alla quantità che produrrà il follower, ovvero sulla base della sua domanda residuale.
Rispetto alla soluzione che si otterrebbe se le imprese si comportassero come nel modello di determinazione simultanea dei prezzi di Bertrand, qui il livello di output prodotto nel mercato è minore e il prezzo di equilibrio è più elevato. Infine, quando entrambe le imprese si comportano come leader, il modello non ammette alcun equilibrio stabile: si genera infatti una “guerra” di prezzo, o di quantità tra le due imprese.
•Oligopolio e teoria dei giochi
La più recente teoria dell'oligopolio ha risentito fortemente degli sviluppi della teoria dei giochi, che si è rivelata strumento potente per l'analisi di situazioni di interazione strategica.
Oggetto di studio della teoria dei giochi è l'analisi di situazioni conflittuali (giochi), in cui uno o più decisori (giocatori) interagiscono, controllando una o più variabili che influiscono sul benessere proprio e degli altri, e determinano congiuntamente il risultato dell'interazione. Scopo della teoria dei giochi è prescrivere che cosa dovrebbe fare ogni giocatore, cioè quale strategia dovrebbe adottare, in modo tale da trarre massimo beneficio dalla propria (parziale) influenza sul gioco. L'opera che ha segnato la nascita della teoria dei giochi come disciplina autonoma è Teoria dei giochi e comportamento economico di J. Von Neumann e O. Morgenstern (1944).
Alla base della nozione di gioco vi è l'interazione strategica fra i decisori.
Una prima distinzione riguarda i giochi non cooperativi e i giochi cooperativi. I primi sono giochi in cui i giocatori non possono effettuare accordi vincolanti fra di loro, mentre i secondi sono quelli in cui tali accordi sono fattibili per certi sottoinsiemi di giocatori, che costituiscono le coalizioni ammissibili.
Per esempio, consideriamo un mercato di oligopolio, in cui n imprese producono un prodotto omogeneo e in cui la domanda di mercato è nota. L'interazione fra gli oligopolisti deriva dal fatto che il prezzo di mercato è congiuntamente determinato dalle decisioni di produzione di ogni oligopolista, e quindi le scelte di produzione di ciascuno contribuiscono a determinare il risultato, in termini di profitti, di tutti gli altri.
Questa situazione è rappresentabile come un gioco cooperativo, se alcuni (o tutti) i produttori (i giocatori) possono concludere accordi di cartello vincolanti fra di loro, cioè contratti che stabiliscano le quote di produzione, oppure il prezzo che deve essere praticato dai membri del cartello, a danno dei consumatori o dei non partecipanti al cartello. Il mercato di oligopolio è invece rappresentabile come un gioco non cooperativo se detti accordi vincolanti non sono consentiti dalle regole del gioco e dunque ogni giocatore agisce in modo autonomo.
•Giochi non cooperativi
Un gioco è costituito da tre elementi: 1) l'insieme dei giocatori (in genere un numero finito); 2) l'insieme delle strategie; una combinazione (o un profilo) di strategie consiste di n strategie, una per ogni giocatore; 3) la funzione di payoff per ogni giocatore; essa associa a ciascuna combinazione di strategie un esito del gioco.
Se il payoff totale relativo alla combinazione di strategie è costante, il gioco è detto a somma costante. Se il payoff è costante ed è pari a zero, il gioco è detto a somma zero. Poiché, nel caso di due giocatori, in un gioco a somma zero, ciò che uno guadagna uguaglia ciò che l'altro perde, si parla anche di gioco a interessi opposti. Se il payoff non è costante, il gioco è detto a somma variabile.
Un gioco è a informazione completa se tutti i giocatori conoscono tutti gli elementi ai punti 1), 2) e 3) e tutti sanno che ognuno è in possesso di questa informazione. Se ad almeno un giocatore non sono noti l'insieme di strategie o la funzione di payoff di altri, diremo che il gioco è a informazione incompleta. Spesso si assume che tutti i giocatori conoscano la struttura del gioco a cui partecipano, siano reciprocamente a conoscenza del fatto che gli altri partecipanti lo conoscano (ovvero, il gioco è conoscenza comune dei giocatori), e inoltre siano razionali, sappiano di esserlo, sappiano che gli altri lo sanno, ecc.
•L'equilibrio di Nash
Nell'ambito della teoria dei giochi non-cooperativi ha un ruolo centrale la nozione di equilibrio proposta dal matematico John Nash (1950).
Un equilibrio di Nash è un profilo di strategie tale che la strategia di ogni giocatore sia una risposta ottimale alle altre. In altre parole, ognuno sceglie la propria strategia migliore, data la strategia che hanno scelto gli altri. Rappresenta i termini di un ipotetico accordo fra i giocatori sul quale conviene a ciascuno conformarsi, se ognuno ritiene che anche gli altri lo facciano. Si parla di equilibrio self enforcing, ovvero ad attuazione spontanea, nel senso che, fintanto che gli altri seguono le raccomandazioni prescritte in equilibrio, non è nell'interesse di alcuno di deviare da quelle.
Per esempio, rappresentiamo un gioco fra due giocatori tramite la tabella (o matrice) sotto riportata, in cui, per convenzione, le righe corrispondono alle scelte possibili del giocatore 1 (siano esse a e ß), mentre le colonne rappresentano le scelte del giocatore 2 (siano esse A e B). In ogni cella, il numero a sinistra indica il payoff ottenuto dalle combinazioni di strategie per 1 e il numero a destra il payoff per 2. Le regole del gioco sono le seguenti: è un gioco one-shot (cioè ogni giocatore deve fare la propria scelta una sola volta); i giocatori scelgono simultaneamente e indipendentemente l'uno dall'altro.
| A | B | |
| a | 10, 10 | 0, 11 |
| ß | 11, 0 | 3, 3 |
La coppia di strategie (ß,B) costituisce un equilibrio di Nash, anche se non è Pareto ottimale (ciò accade nel dilemma del prigioniero, che ha la stessa struttura dei payoffs del gioco). Non sempre esiste un equilibrio di Nash in strategie pure. Tuttavia, estendendo l'analisi alle strategie miste – una strategia mista è una distribuzione di probabilità sulle strategie pure – si può dimostrare che ogni gioco finito ammette un equilibrio di Nash in strategie miste.
Si definisce valore di sicurezza di un giocatore il più alto valore di payoff che egli è in grado di assicurarsi indipendentemente dalle strategie perseguite dagli avversari. Il valore di sicurezza di un giocatore è ottenuto in corrispondenza della strategia detta di maxmin. Nel nostro gioco la scelta di maxmin per il giocatore riga è ß: infatti i minimi delle due righe sono 0 e 3 ed il maggiore dei due è 3, in corrispondenza di ß; dal punto di vista del giocatore colonna la scelta di maxmin è B. Pertanto, la combinazione (ß,B) costituisce la soluzione di maxmin, o di sicurezza, e il valore di sicurezza è (3,3). Applicato a un gioco qualsiasi, il criterio di maxmin, come criterio di soluzione è alquanto arbitrario ed è basato sull'assunto che ogni giocatore i supponga che gli altri giocatori abbiano come obiettivo non il loro benessere, ma il malessere di i. Tale assunzione è giustificata nei giochi a interessi opposti, ovvero nei giochi a somma nulla. Invece, nei giochi a somma variabile, non sempre il valore di sicurezza coincide con la soluzione di equilibrio di Nash.
Media correlati
Figura 12.1a
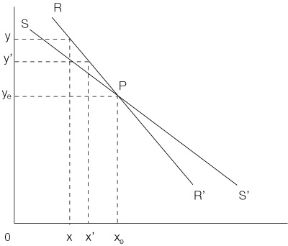
Figura 12.1b Se B offre OY, A reagirà offrendo OX, ma di fronte a questa offerta B offrirà OY' e così via fino al punto P in cui le due curve di reazione si incontrano.


