La dinamica dei fluidi
La dinamica dei fluidi, o fluidodinamica, studia il comportamento dei fluidi in moto, in relazione alle cause che lo determinano. Per ricavare le equazioni che regolano il moto dei fluidi è necessario ricorrere a un modello teorico di fluido, il fluido perfetto, o ideale, supposto del tutto incomprimibile e non viscoso, cioè senza attrito interno. La maggior parte dei fluidi reali non sono fluidi perfetti, ma il loro comportamento, benché a volte si discosti notevolmente da quello dei fluidi perfetti, in molti casi può essere assimilabile a quello dei fluidi perfetti.
Le leggi che descrivono il moto dei fluidi perfetti hanno forme relativamente semplici, che possono venire modificate caso per caso quando si trattano i fluidi reali (i gas, invece, facilmente comprimibili, non sono fluidi perfetti, anche se in certi casi particolari, come nel caso dell'aria in moto a basse velocità, vi si possono avvicinare).
La differenza principale tra un fluido perfetto e un fluido reale è la presenza della viscosità, che tende a ostacolare il moto del fluido imponendo che nelle equazioni del moto siano introdotti termini correttivi che tengano conto della dissipazione di energia causata dall'attrito interno tra le molecole. Inoltre, un fluido reale, a differenza di un fluido perfetto, può presentare due modalità di scorrimento: in un caso può scorrere in strati che scivolano l'uno sull'altro senza mescolarsi (flusso laminare), mentre in un altro caso può scorrere con mescolamento di porzioni di fluido, cioè in modo disordinato e caotico (flusso turbolento), e in queste condizioni le equazioni che ne regolano il moto sono molto più complesse.
Il modo più semplice per studiare il moto di un fluido è quello di incanalarlo in un condotto, di dimensione e curvatura variabile. Si dice che un fluido si muove in regime di moto stazionario quando tutte le molecole del fluido che attraversano una sezione qualsiasi del condotto hanno la stessa velocità in tutti i successivi istanti. Inoltre, nel regime stazionario le molecole del fluido si muovono con la stessa velocità in qualsiasi punto della sezione, indipendentemente dalla distanza dalle pareti.
In regime di moto stazionario i fluidi seguono una legge espressa dall'equazione di continuità, che deriva dalla legge di conservazione della massa, per la quale si può dire che la massa di un fluido che attraversa una sezione di un condotto nell'unità di tempo è costante: in altre parole, in una sezione qualsiasi di un condotto, nel quale non vi siano perdite o guadagni di fluido, si dovrà trovare la medesima quantità di fluido che in qualunque altra sezione. Allora, se m è la massa di fluido che attraversa la sezione di condotto nell'unità di tempo
t, deve essere:
Esprimendo la massa in termini di densità, ricordando che m =
V (dove
è la densità del fluido e
V il volume del condotto di sezione S e di spessore
x) si può scrivere:
Osservando che:
è la velocità del fluido, si può scrivere infine:
che rappresenta l'equazione di continuità. La quantità Sv viene detta portata di massa del fluido in moto e si misura in kg/s; più frequentemente si ricorre alla portata volumica, data da Sv = V/t, che si misura in m3/s.
L'equazione di continuità, applicata a due diverse sezioni S
e dice che in un condotto a sezione variabile in cui scorra un fluido omogeneo con flusso stazionario la portata volumica è costante, ossia quanto maggiore è la sezione del fluido tanto minore è la sua velocità.
Conseguentemente, quando il fluido percorre una strozzatura del condotto la sua velocità aumenta: questo è il motivo per cui negli stretti passaggi o nei tunnel spesso sembra esserci vento, perché l'aria è costretta ad aumentare la sua velocità nel passare attraverso un condotto a sezione minore dell'aria aperta.
Equazione di Bernoulli
La legge fondamentale della fluidodinamica è espressa dall'equazione di Bernoulli, dal nome del fisico francese D. Bernoulli (1700-1782) che la ricavò, ed esprime la legge di conservazione dell'energia nel caso particolare dei fluidi. Si perviene alla legge della conservazione dell'energia considerando un piccolo volume di fluido perfetto che scorre in regime stazionario, con velocità v
Sotto la spinta della pressione pE
E
Il lavoro delle forze di pressione che tendono a spingere il fluido da S
Ricordando le definizioni di energia cinetica e di energia potenziale gravitazionale di un corpo qualsiasi, si ottiene:
Ricordando che il fluido è incomprimibile, per cui:
e introducendo la densità del fluido, si ottiene la forma più comune dell'equazione di Bernoulli (o equazione dell'idrodinamica):
dove p è la pressione che spinge il fluido nel condotto, la sua densità e h l'altezza della sezione. Il termine ?gh, avente le dimensioni di una pressione, rappresenta il peso della colonna di fluido agente su una superficie unitaria e viene detto pressione idrostatica, mentre il termine ?v2/2 viene detto pressione dinamica, esercitata da un fluido per il fatto di essere in movimento con velocità v.
Media correlati
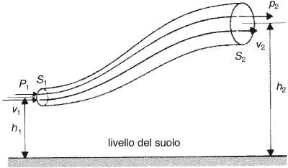
Figura 10.2 Rappresentazione schematica dell'equazione di Bernoulli.


