L'equilibrio
La parte della meccanica che studia le condizioni per cui i corpi, pur essendo soggetti a forze, rimangono in stato di quiete (le condizioni di equilibrio statico), è la statica. La statica riveste importanza nella scienza delle costruzioni perché fornisce gli strumenti per lo studio e la progettazione di tutti i tipi di strutture (case, ponti, dighe ecc.), per cui le condizioni di equilibrio sono ovviamente fondamentali.
Il caso più semplice di equilibrio di un corpo è quello che riguarda il punto materiale. Perché un punto materiale soggetto a forze sia in equilibrio è sufficiente che la somma, o risultante R, delle forze applicate sia nulla, cioè che sia:R = 0. Un punto materiale appoggiato a un piano, per esempio, è in equlibrio rispetto alla forza di gravità perché la forza che la base di appoggio esercita sul punto controbilancia la forza di gravità e di conseguenza la risultante delle forze che agiscono sul punto è nulla.
Quando il corpo è esteso e rigido (si supporrà sempre che i corpi estesi siano rigidi, per semplicità), la condizione che la risultante R sia nulla non è più sufficiente. Un corpo rigido, quale per esempio un libro, appoggiato su un tavolo è in equilibrio perché la forza di gravità determinata dal suo peso è controbilanciata dal tavolo. Ora facciamo ruotare il libro, agendo con le mani su due bordi opposti, applicando due forze di uguale intensità e di verso contrario: in questo caso la risultante delle due forze è nulla e tuttavia il libro non è più in equilibrio. Per equilibrare l'effetto delle due forze, dette coppia di forze, occorre applicare una seconda coppia di forze, che provochi una rotazione uguale e di verso opposto. Una coppia di forze è data da un sistema di due forze parallele, le cui direzioni non sono allineate e sono di verso opposto e agiscono su un corpo mettendolo in rotazione. L'intensità di una coppia di forze è determinata da una grandezza, detta momento della coppia (indicato con M), di intensità M = Fb, dove b è la distanza tra le direzioni parallele della forza, detta braccio della coppia, e F la loro intensità. L'effetto della rotazione è dovuto al momento della coppia. Il momento è un vettore, diretto lungo l'asse di rotazione del corpo a cui viene applicata la coppia, e il cui senso punta verso un osservatore che vede la rotazione in senso antiorario (v. fig. 9.1). In generale, perché un corpo non ruoti occorre che i momenti delle forze che tendono a farlo ruotare in un senso siano compensati dai momenti di forze che tendono a farlo ruotare nel senso opposto, in modo che il momento totale sia nullo, cioè sia:
Perché un corpo rigido sia in equilibrio, devono verificarsi allora due condizioni, cioè che la somma delle forze applicate sia uguale a zero e la somma dei momenti delle coppie applicate sia uguale a zero:
La prima condizione impedisce al corpo di traslare, la seconda di ruotare.
In generale, il momento M di una forza F, applicata in un punto P rispetto a un generico punto O, ha un'intensità data dal prodotto dell'intensità della forza F per la distanza tra il punto di applicazione della forza e il punto O, per il quale passa l'asse di rotazione, ovvero il segmento OP, detto ancora braccio della forza. La direzione del vettore M è perpendicolare alla forza e al segmento OP e il suo verso è dato dalla regola della mano destra (v. fig. 9.2). Il momento di una forza ne misura la capacità di porre in rotazione un oggetto rispetto al punto O. Per aumentare il momento di una forza è sufficiente aumentare il braccio. Il concetto di momento di una forza si applica alle leve , macchine semplici che hanno lo scopo di equilibrare una forza più o meno intensa applicandone un'altra, meno intensa ma di braccio maggiore, in modo da equilibrare i momenti delle forze.
Il baricentro di un corpo
Quando si cercano le posizioni di equilibrio di un oggetto di forma qualsiasi, sia esso appoggiato o vincolato a un punto, nel campo gravitazionale, occorre trovare il suo baricentro, ovvero il punto nel quale si può considerare concentrata tutta la sua forza peso. Il baricentro di un corpo è diverso dal suo centro di massa, che rappresenta un concetto più generale, applicabile anche in assenza di gravità (mentre il baricentro, detto anche centro di gravità, presuppone l'azione della forza gravitazionale). Naturalmente, per gli oggetti con cui si ha normalmente a che fare sulla superficie terrestre, il centro di massa e il baricentro coincidono, dato che il centro di massa è anche il punto di applicazione della forza peso.
La posizione del baricentro di un corpo dipende dalla sua forma geometrica e dalla distribuzione della sua massa. In una sfera omogenea, per esempio, il baricentro coincide con il centro della sfera; in una lamina sottile rettangolare omogenea coincide con l'intersezione delle due diagonali; vi sono anche casi nei quali il baricentro del corpo può essere esterno al corpo. Il baricentro di un corpo può essere determinato attraverso metodi geometrici, se il corpo possiede elementi di simmetria, o sperimentalmente, trovando le posizioni di equilibrio del corpo, se questo è vincolato a un punto fisso (sospeso) o a una superficie (appoggiato).
Equilibrio dei corpi sospesi
Si definisce vincolo tutto ciò che limita la libertà di movimento di un corpo, esercitando sul corpo una forza, detta forza vincolare. Un corpo sospeso è un corpo vincolato a un punto, come, per esempio, un quadro appeso a una parete. L'azione della forza peso del corpo, in questo caso, o di un'altra forza esterna applicata al corpo, può dar luogo solo a un movimento rotatorio. Per trovare le posizioni di equilibrio di un corpo vincolato, occorre trovare il punto in cui la forza peso sia bilanciata dalla forza vincolare, in modo che il corpo non sia libero di ruotare. In particolare, si ottiene l'equilibrio di un corpo sospeso in un punto quando il suo baricentro si trova sulla verticale passante per il punto di sospensione, cioè quando la retta coincidente con la direzione della forza peso del corpo passa per il punto di sospensione. Se si appende un quadro in un punto che non sia il centro di uno dei suoi quattro lati, il quadro ruota, poiché il suo baricentro si trova nel punto che congiunge le sue diagonali, e quindi lungo l'asse che passa per il centro dei suoi lati.
Si può avere equilibrio quando il baricentro si trova al di sotto o al di sopra del punto di sospensione, o anche quando coincide con il punto di sospensione; nei tre casi varranno condizioni di equilibrio differenti. Se il baricentro si trova al di sotto del punto di sospensione (è il caso più comune nell'esempio del quadro, appeso per esempio per il lato superiore, v. fig. 9.3 A), allontanando leggermente il quadro dalla sua posizione di equilibrio il momento della forza peso rispetto al punto di sospensione tende a far tornare il quadro nella sua posizione iniziale. In questo caso si parla di equilibrio stabile. Se invece il baricentro si trova al di sopra del punto di sospensione (v. fig. 9.3 B), allontanando il quadro dalla sua posizione di equilibrio il momento della forza peso tende a farlo allontanare sempre di più dalla posizione iniziale: in questo caso si parla di equilibrio instabile. Il terzo caso, nel quale il punto di sospensione e il baricentro coincidono (v. fig. 9.3 C), è detto di equilibrio indifferente; infatti, il momento della forza peso è nullo perché il punto di applicazione della forza coincide con il punto di rotazione, quindi allontanando il quadro leggermente dalla sua posizione iniziale questo resta nella nuova posizione.
Equilibrio dei corpi appoggiati
Un corpo pesante appoggiato è un corpo vincolato a una superficie. È soggetto alla forza di gravità e alla forza vincolare, diretta verso l'alto, data dalla base di appoggio. Se l'appoggio è in un punto, l'equilibrio si realizza quando il baricentro del corpo si trova sulla verticale del punto di appoggio; anche in questo caso si possono verificare le tre situazioni di equilibrio stabile, instabile o indifferente. Quando, spostando l'oggetto dalla sua posizione iniziale, il baricentro si sposta verso l'alto (v. fig. 9.4 A) l'equilibrio è stabile: il corpo tende a tornare nella posizione iniziale. Quando il baricentro si sposta verso il basso (v. fig. 9.4 B) l'equilibrio è instabile: il corpo si allontana dalla posizione iniziale. Quando infine il baricentro del corpo resta alla stessa quota (v. fig. 9.4 C) l'equilibrio è indifferente.
Nel caso più generale in cui l'appoggio sia in più punti, il corpo resta in equilibrio fino a quando la verticale del baricentro è all'interno della base di appoggio, individuata dalla linea che congiunge i punti di appoggio più esterni (v. fig. 9.4 D). Per questo motivo, un quadrupede è più stabile di un uomo, il quale a sua volta si trova in un equilibrio più stabile se tiene i piedi distanziati. Le auto da corsa, che devono affrontare curve ad alta velocità, sono in genere progettate per avere il baricentro più basso, mentre un camion molto alto è più soggetto a trovarsi in una situazione di equilibrio instabile (nel caso in cui si inclinasse di lato, il suo baricentro rischierebbe facilmente di trovarsi al di fuori della superficie di appoggio).
Media correlati
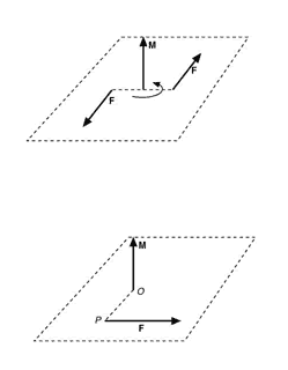
Figura 9.1 Il vettore momento di una coppia di forze.

Figura 9.1 Il vettore momento di una coppia di forze.
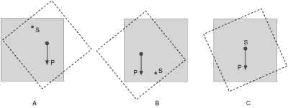
Figura 9.3 Le posizioni di equilibrio stabile (A), instabile (B) e indifferente (C) di un corpo sospeso.
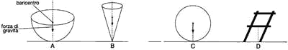
Figura 9.4 Condizioni di equilibrio stabile (A), instabile (B) e indifferente (C) per un corpo appoggiato a un punto di una superficie. Quando l'appoggio è in più punti (D), il corpo è in equilibrio se la verticale del baricentro è all'interno della base di appoggio.


