Lo stato solido

Il reticolo cristallino

La struttura spaziale ordinata delle particelle costituenti un cristallo può essere descritta come un insieme di punti (corrispondenti alle rispettive posizioni) distribuiti regolarmente nelle tre dimensioni, in altre parole con una rappresentazione del reticolo cristallino.

Il reticolo cristallino (v. fig. 10.2) è formato dalla ripetizione di un'unità strutturale (cella elementare) avente una forma geometrica semplice (per esempio, di cubo o parallelepipedo) e caratterizzata dalla lunghezza degli spigoli a, b e c (detti periodi) paralleli a tre assi di riferimento x, y e z (assi cristallografici) e dal valore degli angoli ), nello spazio tridimensionale sono possibili soltanto 14 tipi di celle elementari, 7 fondamentali e 7 da questi derivati. Le 7 celle fondamentali individuano 7 sistemi cristallini, ciascuno dei quali comprende le classi (32) che presentano la comunanza di uno o più elementi di simmetria (v. tab. 10.3). I sistemi a loro volta si suddividono in tre gruppi (monometrico, dimetrico e trimetrico) che si caratterizzano per i valori dei loro periodi (a, b, c).

Tabella 10.3 I SISTEMI CRISTALLINI
gruppo	sistema	costanti cristallografiche	reticolo
monometrico a = b = c	cubico	a = b = c α = β = γ = 90°
	tetragonale	a = b ≠ c α = β = γ = 90°
dimetrico a = b ≠ c	trigonale o romboedrico	a = b ≠ c α = β = γ ≠ 90°
	esagonale	a = b ≠ c α = β = 90° γ = 120°
	rombico	a ≠ b ≠ c α = β = γ = 90°
trimetrico a ≠ b ≠ c	monoclino	a ≠ b ≠ c α = γ = 90° β ≠ 90°
	triclino	a ≠ b ≠ c α ≠ β ≠ γ ≠ 90°
Le 14 celle elementari e multiple a cui si rifanno i corpi solidi cristallini vengono raggruppate in 3 gruppi suddivisi in 7 sistemi che si differenziano in base alla lunghezza a, b, c dei tre spigoli fondamentali e agli angoli α, β, γ che essi formano tra loro.

Media correlati

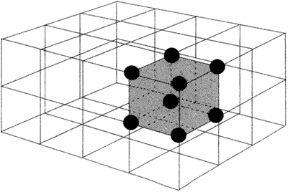
Figura 10.2 RAPPRESENTAZIONE SCHEMATICA DI UN RETICOLO CRISTALLINO E DI UNA CELLA ELEMENTARE

Figura 10.3 ASSI E ANGOLI CRISTALLOGRAFICI